NMR diffusion experiments provide a way to separate the different compounds in a mixture based on the differing translation diffusion coefficients (and therefore differences in the size and shape of the molecule, as well as physical properties of the surrounding environment such as viscosity, temperature, etc) of each chemical species in solution. In a certain way, it can be regarded as a special chromatographic method for physical component separation, but unlike those techniques, it does not require any particular sample preparation or chromatographic method optimization and maintains the innate chemical environment of the sample during analysis. The measurement of diffusion is carried out by observing the attenuation of the NMR signals during a pulsed field gradient experiment. The degree of attenuation is a function of the magnetic gradient pulse amplitude (G) and occurs at a rate proportional to the diffusion coefficient (D) of the molecule. Assuming that a line at a given (fixed) chemical shift f belongs to a single sample component A with a diffusion constant DA, we have:
S(f,z) = SA(f) exp(-DAZ) (1)
Where SA(f) is the spectral intensity of component A in zero gradient ("normal"spectrum of A), DA is its diffusion coefficient and Z encodes the different gradient amplitudes used in the experiment. Depending on the type of experiment, there are various formulae for Z in terms of the amplitude G of the applied gradient and one or more timing parameters such as Δ(time between two pulse gradients, related to echo time) and δ (gradient pulse width). In the original Tanner-Stejskal method using two rectangular gradient pulses, for example,
Z =γ2G2δ2(Δ-δ/3) (2)
The above equation holds strictly for simple PFG-NMR experiments, and is modified slightly to accommodate more complicated pulse sequences. In practice, a series of NMR diffusion spectra are acquired as a function of the gradient strength. For example, the figure below shows the results of a series of 1H-NMR diffusion experiments for a mixture containing caffeine, 2-Ethoxyethanol and water.
It can be observed that the intensities of the resonances follow an exponential decay. The slope of this decay is proportional to the diffusion coefficient according to equation (1). All signals corresponding to the same molecular species will decay at the same rate. For example, peaks corresponding to water decay faster than the peaks of caffeine and 2-Ethoxyethanol
The DOSY transformation
As far as data processing of raw PFG-NMR spectra is concerned, the goal is to transform the NxM data matrix S into an NxR matrix (2D DOSY spectrum) as follows:
The horizontal axis of the DOSY map D is identical to that of S and encodes the chemical shift of the nucleus observed (general 1H). The vertical dimension, however, encodes the diffusion constant D. This is termed Diffusion Ordered Spectroscopy (DOSY) NMR. In the ideal case of non-overlapping component lines and no chemical exchange, the 2D peaks align themselves along horizontal lines, each corresponding to one sample component (molecule). The horizontal cut along such a line should show that components "normal" spectrum. Vertical cuts show the diffusion peaks at positions defining the corresponding diffusion constants. The mapping S=>D will be henceforth called the DOSY transformation. This transformation is, unfortunately, far from straightforward. Practical implementations include mono and biexponential fitting, Maximum Entropy, and multivariate methods such as DECRA. We have recently developed a brand new method for DOSY processing which has been included in Mnova.
Bayesian DOSY Transform
Let´s see how this feature works step by step:
1.Import your raw data: for example by dragging the spectrum folder into Mnova:
2. Process the spectrum: Mnova processes the spectrum automatically for you. However, it might be necessary to apply some further processing, usually manual phase and baseline correction.
You can do that directly on the stacked plot mode, but it´s recommended to use the Active Spectrum mode as depicted below:
Within the 'Active Spectrum' mode, correct any phase distortion and apply an automatic baseline correction (use Berstein polynomials). These corrections will be applied to the whole dataset.
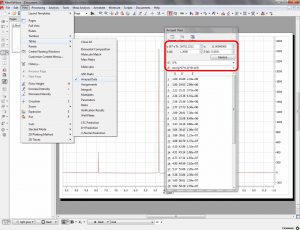
3. Setup Diffusion-related exp. values: Make sure that the big and little delta values have been correctly read from the experiment files by following the menu 'View/Tables/Arrayed Data'. It is possible that these values cannot be properly read (we are still working on this issue). These values should be entered in seconds:

By means of the bayDOSY transform (BDT) we are fitting a model of the type
S(f,z) = SA(f) exp(-DAZ) (1)
where SA(f) is the spectral intensity of component A in zero gradient (normal spectrum of A) and DA is its diffusion coefficient. Z values corresponding to the expression above are displayed in the third column which are calculated according to the formula highlighted in the figure.
It's assumed that the gradient strength come in G/cm. Note that the values used by the algorithm are those listed in the column which are in turn obtained from G column after multiplying these values by the k factor.
4. Run the Bayesian DOSY Transform: Just by following the menu 'Tools/Bayesian DOSY Transform'
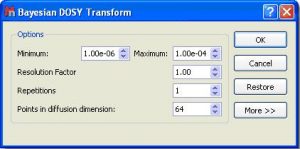
- a) Enter the minimum and maximum expected diffusion values. If the gradient strengths have been introduced in G/cm, the resulting diffusion coeficients will be in cm^2/s
- b) To start with, use a resolution factor of 1 (or 0.1). Higher values will increase the resolution along the diffusion dimension (vertical). However, small peaks can be missed when the resolution factor is too high
- c) The number of repetitions should be kept to 0 for the first try. Next, if you want to further increase the vertical resolution, set this value to 1 or 2. This should drastically increase the resolution, though some artifacts might appear.
This is the result obtained. As you can see the 3 compounds (water,ethoxyethanol and caffeine) are perfectly separated
You can use the 'Crosshair' to measure the Difussion values.
Please bear in mind that Bayesian DOSY Transform is a quantitative method. This will allow you to obtain the relation of each compound by just integrating the diffusion trace.
To do that, just right click on the trace and select 'Setup' in the contextual menu to display the 'Setup Traces' dialog box. Once there click on the 'clue arrow icon to extract the 'Vertical Trace'. Please make sure that this trace is the 'Internal Projection' (Sum)
This will extract the trace to a new page. Finally integrate the signals of this trace to get the corresponding ratio of the compounds: